Differentiability could be a scary-sounding term, but like a lot of math topics once you learn the term it seems simple. It just takes practice! Since I learned about differentiability, I’ve had 100s of hours of experience with it in my engineering career.
As a whole, pure mathematical fractals are not differentiable, however real-life objects with fractal patterns are. Differentiability depends on measuring the smallest edge distance of shapes. Fractal curves are infinite in length and so are not differentiable. Real-life fractals are not infinite.
The concept of differentiability is worth exploring fully. Once the idea is established, it will be easier for you to intuitively think about what that means for fractals. Let’s start with the definition.

What is a Differentiable Function?
Table of Contents
You are probably familiar with the idea of a slope. Just like the average person, I’ve walked up and down slopes my whole life and you have too. What you may not know, is how slopes relate to something being differentiable.
A function is differentiable if the slope exists at every single point. The slope of the function must be calculated using infinitely small steps along the function. This calculated slope is called a derivative, and the branch of mathematics that examines derivatives is called Calculus.
We don’t need to learn all of Calculus to answer our question (this blog post would be very long). Instead, let’s look at some helpful graphs because graphs are always great to see when you’re trying to learn something new about math.
So how do we calculate the slope? You might have heard the phrase ‘rise over run’. This is a simple saying to remind people how the slope is calculated. If I am hiking up a hill, how many steps high did I go up vertically for each step I took horizontally? The equation is pretty simple and looks like this:
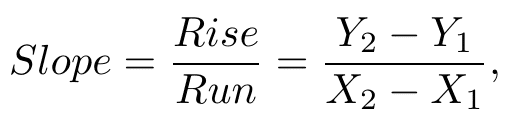
This is the ‘Rise Over Run’ equation to calculate a slope. [1]
If we are calculating the slope of a function, we can take two points and subtract their Y values and X values, divide, and we have our slope. If you play around with this formula, you might notice that the slope value we get depends on which points that you choose.
This is because the slope is an approximation. If you pick two points that are close together, the approximation is better! The slope you calculate is closer and closer to the ‘true’ slope. Check out this graph: suppose that we have the Blue function.
If we start with big steps in our slope approximation (Orange line) we get one answer for the slope value. If we make the steps smaller (Green line) the approximation gets closer to the true slope at each point of the Blue line.
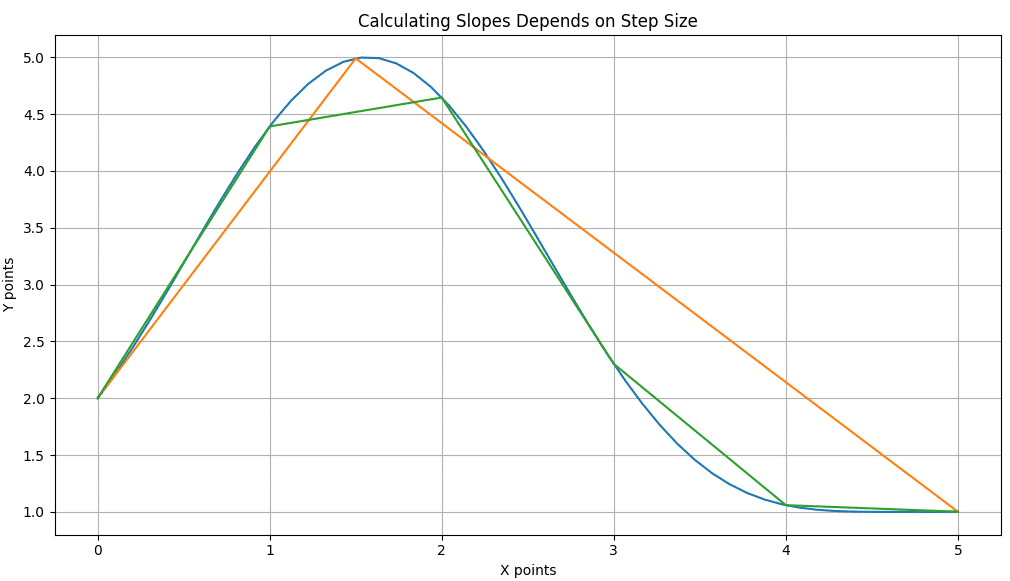
The approximation of the ‘True’ slope gets better as the steps get smaller.
Now, let’s have some fun and get a bit absurd. If the approximation is better when the steps are smaller, what happens if we keep making them smaller forever? If we make the step size infinitely small, this will exactly equal the true slope at every point. The Derivative is what people call the function line that is the true slope of the Blue line.
If it is possible to calculate the derivative at every point, a function is called differentiable. [2]
If it is possible to calculate the derivative at every point, a function is called differentiable.
Awesome! You technically just learned your first basic calculus, nice job. It makes you ask the question though, what kinds of lines and functions aren’t differentiable? Well, usually any function with a hard ‘kink’ in it. The classic example is the absolute value:
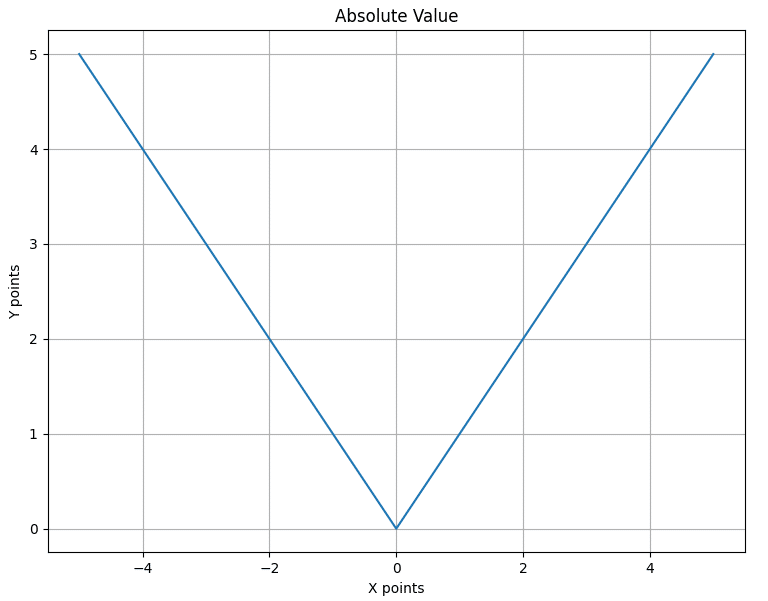
The Absolute Value function is not differentiable.
You might think at first that you can calculate the slope for this. I definitely did when I learned! However, one of the requirements of something being differentiable is that the slope can be calculated at every point. If you look at the point at 0, the slope cannot be calculated.
In the Rise Over Run formula, point 2 has a slope of -1 but point 1 has a slope of 1. Two different values! This means there is no derivative at 0, and the absolute value is function is not differentiable.
So now that we know all about differentiability, can we answer our original question about fractals?
Why Are Fractals Non-Differentiable?
Now that we learned all about what makes something differentiable, the idea generally seems pretty simple. However, fractals look complex and complicated. Fortunately, there is an easy trick to tell if they are differentiable.
As a general rule, fractals are not differentiable. This is due to the property of fractals that they are infinite and fractal curves extend forever. When calculating the derivative, the distance between the points is always infinite even as the step size is made arbitrarily small.
The infinite distance closes the case for mathematical fractals. What about natural fractals that you see in real life? They do not have infinite distance.
Do you like to draw or are you interested in using fractal patterns in your art or designs? Check out my article I wrote about how to draw fractals by hand.

Natural fractal shapes like a fern definitely are differentiable. The self-similarity of the pattern (fern leaf looks like the whole fern) does not extend forever. The fractal shape ends after a certain size and is not infinite. If you were to trace the fern on paper, the edge has a finite length and you can calculate the slope. [4]
Want to know some of the technological uses of fractals? I discussed this aspect of how real life fractals can’t extend forever in my article about fractal technology.
Is there anything special about the most famous fractal?
Is the Mandelbrot Set Differentiable?
The most famous fractal is the Mandelbrot set, so it’s natural to wonder if there is anything that makes it differentiable. Strictly speaking, a set is not something that’s differentiable. If you are wondering this, you are probably asking about the edge of the set which is a function!
As a whole, the Mandelbrot Set is not differentiable. The edge of the set is a fractal curve, and like other fractal curves it has an infinite length. The edge contains infinite detail and that makes it impossible to measure a slope at every point on the edge.

Even though the edge has no derivative and infinite detail, the edge is unbroken and continuous. Normally, when something is differentiable, it automatically implies that it is also continuous. [3] Is there anything else that is continuous but also not differentiable?
If you want to learn more about the Mandelbrot Set, check out my post about the famous fractal. Are you interested in the history of fractals and their use in art? Check out my article taking a deep dive on fractals in art!
What is Continuous but Not-Differentiable?
We learned about how the absolute value function is continuous but has a single point that is not differentiable. Many of the functions are like this example and have single points or regions which are continuous and not differentiable. There is one class of functions which can be both everywhere!
As a whole, fractals are the class of functions that are continuous but not differentiable. Fractals like the Weierstrass function were historically specifically defined to be continuous and not differentiable everywhere.
Originally, the Weierstrass function was invented to debate the ideas around continuous functions in the 1800s. It was not until much later that the function was identified as a fractal. I found out mathematicians are still making new discoveries as recently as 2018! [5]
Tons of these mathematical details are discussed in Mandelbrot’s books. Want to know more? Check out my complete list of Mandelbrot’s books.
Finale: Fractals and Differentiability
Fractals are fascinating to visualize and explore. Hopefully, now that you know all about their differentiability properties it will enable you to appreciate their uniqueness mathematically too.
If you would like to learn about fractals generally, check out my post about the history of fractals.
Interested in reading more about Fractals? Check out some other posts in the Fractal Category.
Get Notified When We Publish Similar Articles
References
- “Slope.” Wikipedia, Wikimedia Foundation, 5 January 2022, https://en.wikipedia.org/wiki/Slope.
- “Differentiable Function.” Wikipedia, Wikimedia Foundation, 27 January 2022, https://en.wikipedia.org/wiki/Differentiable_function
- Mandelbrot, Benoit B., and Benoit B. Mandelbrot. The fractal geometry of nature. Vol. 1. New York: WH freeman, 1982.
- Avnir, David, et al. “Is the geometry of nature fractal?.” Science 279.5347 (1998): 39-40.
- “Weierstrass_function.” Wikipedia, Wikimedia Foundation, 4 November 2021, https://en.wikipedia.org/wiki/Weierstrass_function.

