The famous images of fractals that we all know are stunning to look at, but you might be left wondering like I was – what are some of the uses of these fractals in technology? How does it affect my life? I combed through piles of science and engineering research to find some of the highest impact uses!
As a general rule, fractals have many uses in technology. The most consequential uses include cell phones, antennas, transistors, signal processing analysis, and heat exchangers. Fractals enabled cell phone miniaturization by replacing large antennas with higher quality compact versions.
The practical uses in technology are almost as infinite as the fractal shapes themselves. Let’s explore the details of how these shapes are applied so you understand how fractals favor your tech. You see the most important use every day!
Fractal Antennas: Enabling Tiny Cell Phones
Table of Contents
The most important use of fractals by far is in antenna technology. During the late 1990s and early 2000s, researchers discovered this antenna shape which delivered higher quality signals across a wider band of frequencies. The key innovation was the fractal shape which is self-similar. [1]
This self-similar property of fractal shapes means that the antenna can operate in the same way at different scales. For example, the Vicsek Antenna is shaped like a square consisting of tiny squares, that themselves consist of tiny squares. This allows signals that are 100 MHz, 1000 MHz, or 10000 MHz to all resonate and interact with the antenna in the same way. [2] The engineer designs the square sizes for each application.
Before the invention of fractal antennas, the engineers making them needed to design the antenna length to operate at the specific frequency of the device it was attached to. This was the main reason early cell phones had the ‘pull-out’ long and straight antenna which extended to the needed operating length.
The special self-similar shape also allowed the use of new beamforming techniques. [3] Beamforming is the practice of ‘steering’ the signal in a direction rather than having it transmit from the antenna outward in a sphere. Think shining a flashlight vs. using a lantern. Beamforming is used in sound recording systems where a specific sound source (like a singer on stage) must be recorded. Beamforming is also used in 5G cell towers to give the user a high-speed directed connection to the tower.
I once got the privilege of seeing an audio engineer beamform a giant speaker! Only the area it pointed to vibrated with sound.
Another popular antenna choice is the Sierpinski Triangle. Want to learn how to make or draw these antenna shapes? Check out my beginner’s guide about creating these fractals by hand!
Uses of Fractals in Electronics
Fractals have other uses in electronics, but they probably aren’t uses that you can see! Tiny transistors within the electronic circuits can have fractal shapes for similar reasons as the antennas.
They allow the transistor to operate over a greater range without any loss in performance. [4]
Common consumer devices that make use of fractal transistors are [5]:
- Phones
- Microwaves
- Radar
- Satellite TVs
- Voltage Converters
- Low Power Amplifiers
The general class of this fractal-based transistor is called a High Electron Mobility Transistor (HEMT). [6]
One of the advantages of this fractal method for creating the transistors was that the self-similarity allowed the engineers to predict some of the characteristics needed to manufacture the device. [6] For example, suppose we used the square antenna example from above. You already know the next square size will allow a signal 10 times the frequency to be picked up by the antenna, so if you need to receive that signal you already know how big the square needs to be. This technique is also used in manufacturing semiconductor components. [7]
One of the advantages of this fractal method for creating the transistors was that the self-similarity allowed the engineers to predict some of the characteristics needed to manufacture the device.
Signal Processing Applications
There are numerous signal processing techniques related to fractals as well. Signal processing is the technique of analyzing some data that was collected over time and extracting important patterns. The use of fractals in this field also comes from the self-similar property of fractals. [8]
Some examples that you might be familiar with are harmonics and octaves in music. The sound waves produced at different octaves are similar to each other, only scaled to a different size. A ‘C note’ at one octave is a self-similar sound to a ‘C note’ at a different octave.
Observe how with price signals, data collected at 1-hour intervals is self-similar to data collected at 1-day intervals. Without the time scales labeled, it is impossible to distinguish which is which. Price signals are widely considered to be fractal and were an intense focus of study for the mathematician Benoit Mandelbrot.
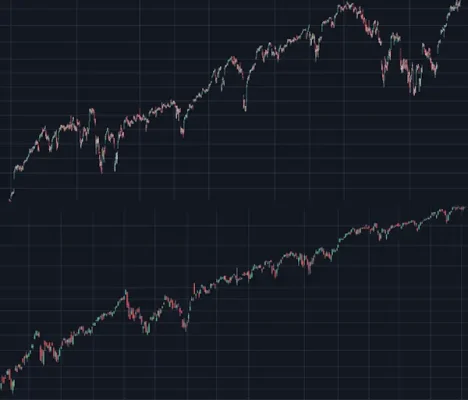
Fractal signals are signals that exhibit self-similar behavior, and the data points for fractal signals look the same at different time scales. Analysis techniques for examining the properties of fractal signals exist for both real-time processing and post-processing the data.
These fractal signals do not need to repeat the self-similar property forever. In real life, signals are not perfect. Even if they were, the electronic sensors which exist for recording data are not perfect and measurement error prevents the pattern from repeating forever. [9]
Curious whether the fractal pattern repeats forever in real life? I completely cover this aspect in my article about whether fractals are differentiable. I also discuss how natural fractals appear all around us in nature in my post on fractals in nature!
The function of fractal analysis is to identify what characteristics of fractals exist in signal data and use those properties to compare the signal from different fields. For example, the fractal properties of heart rate data can be compared directly to sound signals.
Using modern techniques, fractal analysis can be performed in real-time as the data is collected. [10]
Want to know more about Mandelbrot’s mathematical innovations in finance and explore some of his useful tools? Check out my complete list of Benoit Mandelbrot’s books! If you want to know more about the Mandelbrot Set, check out my post about the famous fractal that bears his name.
Fractals Used in Heat Exchangers
A heat exchanger is a device used in engineering applications to transfer extra heat from something hot to something cold so that the device generating the heat can keep operating normally. They come in many different shapes and sizes, and the heat exchanger is often designed for the specific application where it will be used. A common example you might be familiar with is a car radiator.
The advantage of a heat exchanger is that the device which is being cooled can continue to maintain operation and maintain its performance at the level it was designed for. For example, the heat exchangers which are on CPUs in computers keep the chip from overheating and shutting down while you work.
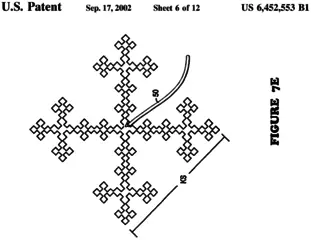
Heat exchangers with a fractal pattern have been explored and deliver similar results to exchangers without the pattern, only they often use much less material! Fractal heat exchangers can follow the Koch Snowflake pattern seen above. [11] This is fantastic for applications where weight is a factor because it can affect the performance to have too much weight. For example, fractal heat exchangers have been investigated for use in planes. [12]
Fractal heat exchangers can also help reduce the cost of the heat exchanger in cases where many exchangers need to be manufactured. If less material and less weight are used, that is less cost!
Looking for artistic applications of fractals? Check out this article I wrote doing a deep dive into fractal art!
If you would like to learn about fractals generally, check out my post about the history of fractals.
Interested in reading more about Fractals? Check out some other posts in the Fractal Category.
Get Notified When We Publish Similar Articles
References
- “Fractal Antenna.” Wikipedia, Wikimedia Foundation, 3 February 2022, https://en.wikipedia.org/wiki/Fractal_antenna
- Cohen, Nathan. “Fractal antenna applications in wireless telecommunications.” Professional Program Proceedings. Electronic Industries Forum of New England. IEEE, 1997. https://www.academia.edu/download/39422672/00605374_1.pdf
- Werner, Douglas H., and Suman Ganguly. “An overview of fractal antenna engineering research.” IEEE Antennas and propagation Magazine 45.1 (2003): 38-57. https://ieeexplore.ieee.org/abstract/document/1189650
- Reiner, Richard, et al. “Fractal structures for low-resistance large area AlGaN/GaN power transistors.” 2012 24th International Symposium on Power Semiconductor Devices and ICs. IEEE, 2012. https://ieeexplore.ieee.org/document/6229091
- “High-electron-mobility transistor.” Wikipedia, Wikimedia Foundation, 21 January 2022, https://en.wikipedia.org/wiki/High-electron-mobility_transistor
- Torkhov, Nikolay A., Leonid I. Babak, and Andrey A. Kokolov. “The Influence of AlGaN/GaN Heteroepitaxial Structure Fractal Geometry on Size Effects in Microwave Characteristics of AlGaN/GaN HEMTs.” Symmetry 11.12 (2019): 1495. https://www.mdpi.com/2073-8994/11/12/1495/pdf
- Reiner, Richard. “Semiconductor component comprising at least one contact structure for feeding in and/or leading away charge carriers.” U.S. Patent No. 9,577,056. 21 Feb. 2017. https://patentimages.storage.googleapis.com/02/93/1a/1b224dc7cef197/US9577056.pdf
- “Fractal analysis.” Wikipedia, Wikimedia Foundation, 6 February 2022, https://en.wikipedia.org/wiki/Fractal_analysis
- Levy-Vehel, Jacques. “Fractal approaches in signal processing.” Fractals 3.04 (1995): 755-775. https://hal.inria.fr/inria-00593322/document
- Hartmann, András, et al. “Real-time fractal signal processing in the time domain.” Physica A: Statistical Mechanics and its Applications 392.1 (2013): 89-102. https://www.academia.edu/download/55248105/Hartmann-et-al__Physica-A__Real-time-fractal-processing_2012.pdf
- Meyer, Josua P., and Hilde Van Der Vyver. “Heat transfer characteristics of a quadratic Koch island fractal heat exchanger.” Heat transfer engineering 26.9 (2005): 22-29. https://www.academia.edu/download/45591424/71_Meyer_and_Van_Der_Vyfer_2005.pdf
- Torrez S. “Fractal Heat Exchanger for Gas Turbine Pre-Cooling” Physical Sciences. Solicitation. https://www.sbir.gov/node/1410833