Using fractals in projects is a lot of fun. This beginner’s guide will get you started learning how to draw fractals by hand.
Math and algorithm-based art may seem to be a futuristic vision, but it is a growing and widely found concept.
Fractal art isn’t a new idea. It’s been hanging around since the 1980s. Fractal art has recently seen a resurgence. More and more designers are turning to it for backgrounds, key art components, and interior design elements.
Fractals Generally
Table of Contents
- Fractals Generally
- Self-Similarity: Key to Drawing Fractals
- Using Fractal Art in Your Own Projects
- Learning How to Draw the Easy Fractals by Hand
- How to Draw Fractals on Paper: Creating Custom Fractals
- Examples in Nature
- Art Techniques for Creating Fractal Elements
- Final Thoughts: How to Draw Fractals by Hand
- References
Fractals are based on arithmetic and geometry, as well as visual design. A fractal element, by definition, is a geometric pattern that is replicated on bigger and/or more minor scales to produce visually appealing irregular forms and patterns. Fractals are never-ending patterns that repeat themselves.
Many fractals are based on natural phenomena, such as how the Fibonacci sequence (arithmetic) relates to the nautilus shell (nature). Another easily recognized fractal is the mandala.
Natural fractals can include river networks, blood vessels, seashells, lightning bolts, galaxies, tree limbs, and hurricanes.
Fractals can be found in nature, created by mathematical formulas or algorithms, or drawn by hand. Most modern digital fractal art is made using computations and an algorithm to produce an animation, still image, or another sort of “living” media. The vast majority of modern fractal art graphics are abstract motifs with a clearly digital-generated look and feel.
Fractals can be utilized in design to create stunning individual pieces of art or great background patterns. Fractal art is not only visually appealing but soothing and stress-relieving.
In the movie industry, fractals are helpful for generating natural-looking landscapes and planetary terrains. An algorithm can be designed to formulate complex visual imagery to replicate fractals in nature to create computer-generated images of rivers.
Fractals have been used more successfully in constructing the Internet’s networks, explaining financial markets, understanding astronomy and DNA, and even diagnosing some diseases!
Self-Similarity: Key to Drawing Fractals
Fractals are created by recursion. Recursion is a problem-solving and programming technique in which the main problem is solved by dividing it down into smaller chunks of the same problem. The minor problems are identical to the major problem and can thus be tackled using the same method.
Fractals can have a geometric shape or may contain multiple forms. They can also have irregular curves and asymmetrical shapes. If you zoom in on more extensive, complex fractals, you may be surprised to find smaller pieces of art within.
Mathematical fractals are created by calculating simple equations in repetition. Arithmetic fractals are infinitely complex, meaning that they can continue forever.

Using Fractal Art in Your Own Projects
Fractal art can be used in a variety of ways in design projects. The very first step is to determine if a still or dynamic fractal art element is required.
Then you can employ them in everything from a web page background to a hero video to a component of a complex visual collage to create a design theme by integrating fractals with other design details.
The most important thing to remember about most fractal art arrangements is that patterns can be pretty intense and should almost always be regarded as a dominant element. Otherwise, you risk having competing parts in your design, making it difficult for the viewer to understand visually.
Another alternative is to use a faded fractal art background to add dimension and depth without being too overbearing. This might be an excellent place to start if you really want to try your hand at fractal art.
Learning How to Draw the Easy Fractals by Hand
Learning how to make fractals by hand can be quite the undertaking, but once you get the hang of it, you can doodle your way to beautiful works of art. Let’s cover how to draw a few common fractals step-by-step.
The Sierpinski Triangle (Sierpinski Gasket)
Defined almost one hundred years ago in 1915, the Sierpinski Gasket is extremely popular. It can be found in 13th-century mosaics, the top levels of Pascal’s triangle, and even in popular video games. [1]
Each set of triangles is repeated in a pattern. When the triangles are repeated at a new size, it is called an iteration. An iteration is repeating an identical operation. This technique of iteration will be used in the drawing instructions of all fractal patterns. This can be repeated until it is as small as medium allows.
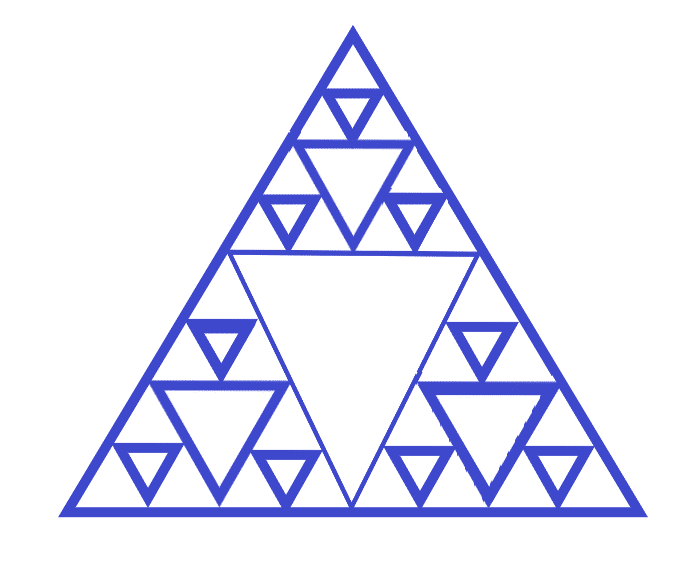
- First, draw an equilateral triangle (a triangle whose sides are all of equal length with sixty-degree angles all the way around).
- Draw a single dot in the middle of each side of the equilateral triangle. Connect these three points with a line to create a new triangle within the original triangle. You now have four smaller triangles, one in the center and three on each side. The central triangle points downwards, while the other three triangles face upwards.
- Repeat step two for the three upward-facing triangles. Make new triangles by drawing a point in the center of each side of the three upward-facing triangles and connecting each with a line.
If you were to stop the iterations on your Sierpinski Triangle, you would have one sizable downward-pointing triangle in the center flanked by three smaller downward-pointing triangles. You could shade the upward-pointing triangles in a dark color, such as black, and the downward-pointing triangles in a contrasting shade, such as white.
If you continue your iterations by drawing a point in the center of the sides of the upward-facing triangles and linking the points with a line to continue to create new triangles, you will continue to increase the number of upward- and downward-facing triangles throughout your Sierpinski Triangle.
The Koch Snowflake
The Koch Snowflake, which is based on the Koch curve, is one of the first fractals ever explained. The methods used to create the snowflake are comparable to those used to measure oceanic coastlines. [2]

- Start by drawing an equilateral triangle (equal sides, sixty-degree angles).
- Each side of your triangle should be divided into thirds. Remove the third from the middle of your triangle and draw two sides of another equilateral triangle over it (connected to the other two sides). To put it simply, replace the line with a peak. Your new shape will have twelve sides (or six connected points).
- Repeat step two on each of the twelve sides of your new shape. After completing the iteration, your form will have forty-eight sides.
If you continue another iteration, your shape will have one hundred ninety-two sides. You can continue repeating step two (iterations) as long as you choose. The more iterations you complete, the more complex your Koch Snowflake will be.
Do you want to know how fractals are used in common technology? I discussed how the Koch Snowflake is a common shape for fractal antennas and fractal heatsinks in my post about fractal technology.
The Harter-Heighway Dragon (Dragon Curve or Jurassic Park Fractal)
The Jurassic Park fractal is the youngest fractal that we’ll draw together. Once finished, you might recognize this fractal from the well-known book Jurassic Park.
The number of lines necessary to generate the Dragon’s Curve doubles with each iteration. It is vital to completely duplicate the previous iteration and attach it to the last line at all times. [3]
- Start by drawing a single line. Copy your line (length, width), rotate it clockwise (ninety degrees), and attach it to the end of your first drawn line.
- You now have an L-shaped line. Copy the entire L-shaped line (length, width), rotate the copy clockwise (ninety degrees), and attach it to the end of the original line.
The number of lines required to draw The Dragon Curve doubles with each repetition. It’s critical to spin a duplicate of the previous form (length and width) and attach it to the end of the earlier iteration at all times. - You should now have a backward question mark. Copy the entire line, rotate it clockwise, and link it to the end of the line created by step two.
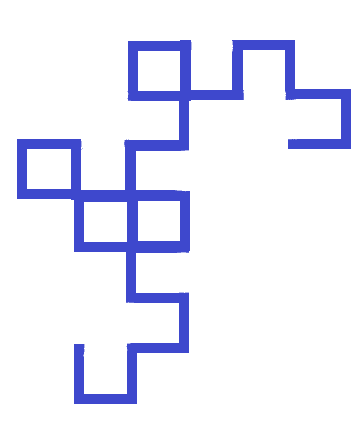
- Now, you will repeat step three for the entire line created by previous iterations.
Your rotated line segments will intersect with the last line and form a square box. While this fractal will never cross over itself, there will be intersections such as this throughout. - Continue repeating step three with the whole line you’ve created.
By this fifth iteration, you should start to have an idea of the entire shape of the Dragon’s Curve. - Iterations can continue until you are satisfied with the fractal design.
The Hilbert Curve
The Hilbert Curve is a deviation of the Peano curve. The uses of this fractal stem into model manufacturing and modern technology. [4]

- First, draw the bottom and two sides of a square. Your drawing should look like a square-based letter U with three equal distance lines. This is the initial stage of the Hilbert Curve.
- Stage two begins when you make a mirror image of the initial stage to the right of your first drawing, leaving a gap equal to the length of one of the line segments between them.
- Draw a copy of the image on the left and rotate it ninety degrees counter-clockwise, leaving a gap equal to the length of one of the line segments between the shapes.
- Draw a copy of the image on the right and rotate it ninety degrees clockwise, leaving a gap equal to the length of one of the line segments between the shapes.
- You will now have four unconnected U-shapes.
- Connect the four U-shapes with three straight lines. This completes stage two.
- Each stage of the Hilbert Curve is an iteration of steps one through six, creating more extensive and more intricate groupings of lines.
The Pythagorean Tree
The Pythagorean Tree is created by a series of squares. Though it is simple to develop, the completed fractal is pretty amazing! [5]
- Start by drawing a 1”x1” (or larger) square towards the bottom of your paper or canvas.
- Draw a right isosceles triangle (a right-angled triangle whose base length and height are equal) with the base (hypotenuse) serving as the top edge of your square.
- Create two squares along the legs of your isosceles triangle. The leg of the triangle will serve as the base of the square.
- Repeat steps two and three, drawing squares and triangles respectively, until you are satisfied with the size of your Pythagorean Tree.
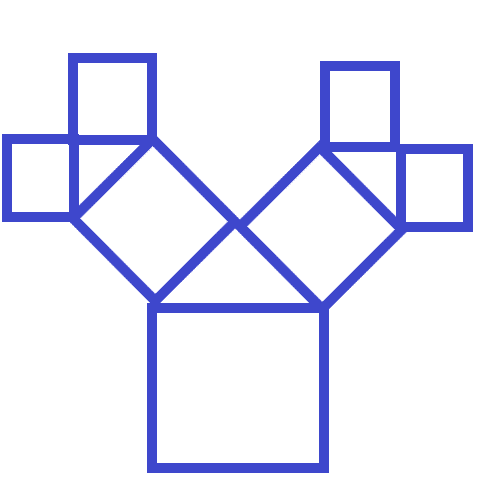
Be sure that the initial square is no smaller than 1”x1”. If you begin with a square that is too small, it will definitely increase the difficulty level of learning how to draw the Pythagorean Tree. It is also advisable to utilize a ruler to ensure clean, straight lines.
Interested in some of the mathematics around fractals? Check out this post about whether fractals are differentiable.
How to Draw Fractals on Paper: Creating Custom Fractals
You can create your own custom fractals by following these simple step-by-step directions:
- You first draw a larger version of a geometric shape or print that you would like to be replicated within itself.
- Choose a repeating rule (line connection, rotation, etc.).
- Apply your chosen rule to the print or geometric shape.
- Repeat until you feel that your fractal art is completed or until you can no longer successfully fit any more repetitions into your fractal.
Examples in Nature
The laws that control the development of fractals appear to exist everywhere in nature. Pineapples develop according to fractal rules. Snowflakes form in fractal patterns, similar to those found in river deltas and your body’s veins. It’s commonly claimed that Mother Nature is an incredible designer, and fractals are the design principles she employs.
Fractals are highly efficient, allowing plants to increase their exposure to the sun and circulatory systems to carry oxygen to all regions of the body as efficiently as possible. There are many beautiful examples of fractals found in nature, from the weather in the skies to the underground roots of plants.

A few natural fractals are:
- Romanesco broccoli
- Pine cone seeds
- Leaf venation
- Dendritic copper crystal formation
- Ice crystal formation
- River and tributary systems
Art Techniques for Creating Fractal Elements
Fractal art comes in many different forms. Some common elements can be grouped into the following:
- Standard geometry derived
- Iterated function systems
- Points and patterns of strange attractors
- Fractal flame
- Realistic L-system fractals
- Famous complex polynomial iterations
- Newton fractals
- Pure mathematics quaternionic fractals
- Fractal terrains
- Three-dimensional mandelbulbs
Interested in learning more about Benoit Mandelbrot? He is the namesake of the Mandelbulb. Check out my complete list of Mandelbrot’s books! If you would rather learn about the 2D Mandelbrot Set, check out my post on the famous fractal.
When it comes to designing fractal art, science and technology play an essential role. Some are made by solving nonlinear equations with iterative approaches. That is why the job of creating many fractal designs is carried out by computers.
To learn the rich history and legacy of fractal art check out a comprehensive overview of the topic.
Final Thoughts: How to Draw Fractals by Hand
Fractals can be absolutely beautiful and soothing to draw. Hopefully, these step-by-step directions will enable you to create your own beautiful works of fractal art.
If you would like to learn about fractals generally, check out my post about the history of fractals. Fractals also frequently appear in natural patterns. Check out my deep dive about fractals in nature!
Check out some other posts in the Fractal Category to learn more on this endlessly fascinating topic.
Get Notified When We Publish Similar Articles
References
- “Sierpinski Triangle.” Wikipedia, Wikimedia Foundation, 14 January 2022, https://en.wikipedia.org/wiki/Sierpi%C5%84ski_triangle.
- “Koch Snowflake.” Wikipedia, Wikimedia Foundation, 5 January 2022, https://en.wikipedia.org/wiki/Koch_snowflake
- “Dragon Curve.” Wikipedia, Wikimedia Foundation, 5 October 2021, https://en.wikipedia.org/wiki/Dragon_curve.
- “Hilbert Curve.” Wikipedia, Wikimedia Foundation, 10 September 2021, https://en.wikipedia.org/wiki/Hilbert_curve.
- “Pythagoras Tree (Fractal).” Wikipedia, Wikimedia Foundation, 17 July 2021, https://en.wikipedia.org/wiki/Pythagoras_tree_(fractal).