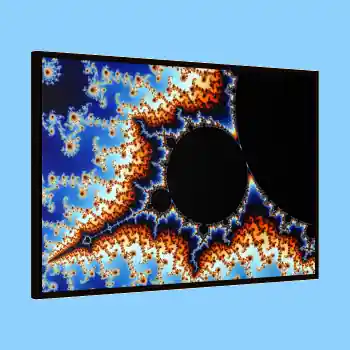
A fractal is a form of an infinitely complicated mathematical shape. In general, a Fractal is a pattern that repeats continuously, and every section of the fractal, no matter how zoomed in or out, appears to be identical to the original shape. So you may come to wonder, who discovered the fractals? In this article, I will discuss everything you need to know about the history of fractals in detail.
Pierre Fatou and Gaston Julia discovered fractals while studying complex mathematical systems at the turn of the 20th century. Considered mathematical monsters with unlimited complexity, fractals resisted linear analysis. Fractals were forgotten until Benoit Mandelbrot published his work in the 1960s.
Mandelbrot coined the term “fractal” while working at IBM’s Armonk, New York labs. He solidified hundreds of years of thought and mathematical growth and illustrated his formal meaning with spectacular computer-constructed images. These visuals, such as his iconic Mandelbrot set, captivated the public imagination; many were based on recursion, giving rise to the popular interpretation of the term “fractal.” Keep on reading to learn more about its invention, types, generating techniques, and usage.
Who Invented Fractals?
Table of Contents
Many people can remember when they first saw a fractal image. I first heard of fractals when my high school friend found pictures of them online. They of course were created much earlier than that.
Fractals have a long history, beginning with theoretical research and progressing to modern computer graphics applications, with several notable persons providing archetypal fractal forms.
The use of fractal scaling, in which minor structure elements tend to look identical to more significant parts, is a common subject in traditional African architecture, such as a circle community made up of circular houses. [1]
Early Days Of Invention
The earliest point on the fractal timeline starts in the 17th century. One of the most famous mathematicians and philosophers of the time Gottfried Leibniz contemplated recursive self-similarity.
He used the term ‘fractional exponents’ to refer to the scaling properties.
The historical record also says he believed that just a straight line was also self-similar, but in our modern understanding, we do not consider that a fractal. [2]
Unfortunately for us, interest in fractal issues and topics waned after Leibniz. The few who studied the topic called them “mathematical monsters.” [2]
First Definition of Fractal
Our next stop on the fractal timeline jumps us forward to the 18th of July, 1872.
At the Royal Prussian Academy of Sciences, Karl Weierstrass discovered a special function that is now named after him.
This function is everywhere continuous but nowhere differentiable. If you want to learn more about this topic and how it relates to fractals, check out my post on whether fractals are differentiable.
Georg Cantor, a student who would later become a mathematician, had attended Weierstrass’ lectures.
He studied subsets of the real line that we now call Cantor sets. These lines are self-similar and follow the pattern by removing sections. We consider the Cantor set to be a fractal pattern today.
Self-Inverse Fractals
In the late 1800s, Henri Poincaré and Felix Klein discovered what we now call “self-inverse” fractals. [3]
In 1904, Helge von Koch disliked Weierstrass’ definition that fractals were continuous but not differentiable. He began with Poincaré’s ideas and instead suggested a definition from geometry. He created hand-drawn images of an identical repeating pattern that we now know as the Koch snowflake. Want to learn to draw fractal patterns like Koch? Check out my post on how to draw fractals by hand.
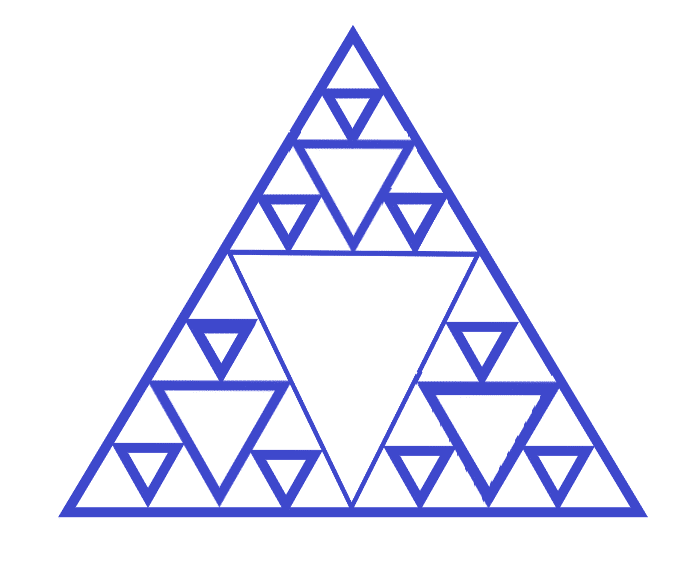
The next stop on the timeline is slightly over a decade later. In 1915, Waclaw Sierpinski created what we call the Sierpinski Triangle today. You can also learn to draw this triangle using my guide.
A few years later the field of fractals started to take a more solid theoretical shape. Two French mathematicians, Gaston Julia and Pierre Fatou started to relate their studies of dynamics, attractors, repellors, and the complex number plane. Today we call this field Chaos Theory. These two arrived at essentially identical results using iterative functions and complex numbers.
Evolution of the Definition of Fractals
The very same year, Felix Hausdorff made another important contribution to the field of fractals. One important characteristic is there is a measurement of the dimension which we call the Hausdorff dimension. Fractals can have non-integer dimension like 2.5 or 3.1 instead of 2-D or 3-D.
Paul Lévy made important contributions to stochastic processes, random walks, and probability. Related to this study, he expanded on self-similar curves we now call the Lévy C curve.
One unfortunate fact of the fractal investigations so far is that they were limited by the technologies of their time. Some fractals like Cantor’s and Sierpinski’s fractals can be created with drawings, however, some fractal studies require the aid of computer graphics.
Want Your Own Fancy Fractal Art? – I’ve Got You Covered!
Discover the most eye-popping artwork, clothing, and dog beds. Stop wasting time searching for less exciting alternatives! Impress your friends and loved ones while supporting the site in the process
Benoit B. Mandelbrot: Father of Fractals
Benoit B. Mandelbrot, a Polish-born mathematician had Paul Levy as an academic advisor. Mandelbrot invented the term fractal and named it from the Latin word fractus, which means “broken” or “fragmented.”
Mandelbrot originally used printers to create the graphics that he required to study the fractal dynamics of attractors. Later, he would use computer screens as the technology caught up with his ideas.
If you want to read some of Mandelbrot’s fascinating books, check out my complete list!
Mandelbrot used fractal ideas to advance the study of physical objects, probability, stock market behavior, and dynamics. As I discussed in my post about how fractals are used in technology, fractal geometry also drove the miniaturization of cell phones.
Loren Carpenter created software in 1980 for producing and visualizing fractally cultivated landscapes. This method is used often today to generate realistic-looking landscapes in video games.
| Mathematician | Timeline Date | Discovery |
|---|---|---|
| Gottfried Leibniz | 1650-1700 | Discovers self-similarity |
| Karl Weierstrass | 18 July, 1872 | Invents Weierstrass function |
| Georg Cantor | 1883 | Discovers Cantor Set Fractal |
| Henri Poincare and Felix Klein | 1880s | Creation of Self-Inverse Fractals |
| Helge von Koch | 1904 | Makes and presents the Koch Snowflake |
| Waclaw Sierpinski | 1915 | Invention of the Sierpinski Triangle |
| Pierre Fatou and Gaston Julia | 1918 | Study iterative functions and dynamics |
| Felix Hausdorff | 1918 | Creates the measurement of Hausdorff dimension |
| Paul Levy | 1938 | Creation of the Levy C Curve |
| Benoit Mandelbrot | 1960s | Develops cohesive fractal theory in a series of papers |
| Benoit Mandelbrot | 1975 | Coins the term Fractal |
| Loren Carpenter | 1980 | First Fractal Landscape rendered |
What Are Fractals Used For?
Fractal mathematics has numerous applications, including chaos theory and the study of complex dynamic systems, creating spectacular computer images, compression of computer files, studying the architecture of the internet’s networks, and even the diagnosis of various diseases.
The uses are wide-ranging and are encountered frequently in our day-to-day lives.
Fractals In Geometry
Fractal geometry and the ability to measure the Hausdorff dimension of collected data may be used to comprehend the complexity of systems and shapes.
Fractal geometry can describe unpredictable phenomena in various ways.
These types of distributions are called Power Laws and were a favorite subject of study for Levy. These include earthquake timing and size, variations in a person’s heartbeat, and the occurrences of diseases and death.
Fractals In Art
Fractals can also be used in arts. The image formed by a fractal is intricate yet striking, and it has long piqued artists’ interest.
Studies have shown artists such as Jackson Pollock and Max Ernst produce seemingly chaotic yet defined structures.
Their artwork has been shown to have a measurable Hausdorff dimension. I talked all about this in my guide about Jackson Pollock.
If you want to check out some of the other ways fractals are used in art, check out my post that does a deep dive into the subject.
Fractals In Biology
Furthermore, fractals have a significant role in biological research. Sometimes, natural systems can follow fractal shapes.
For example, blood vessels have a self-similar structure. The ability to measure their fractal shape allows our scientists and doctors to create better treatments for patients.
Fractals can also model other networks like neurons and the nervous systems of various animals. Bacterial growth can also follow a self-similar scaling and so exhibits fractal patterns.
Fractals In Imaging
One of the most common applications of fractals is image compression. The pixel data in an image can be expressed as an iterated system of functions. This allows for the storage of the image to be recorded as a much smaller number of parameters. This image still appears fast and renders itself in great detail at any magnification (due to the scaling property of fractals). [4]
There is nothing more to this than a simple iterative formula. It is so simple that most children can program their home computers to produce the Mandelbrot set. … Its astounding complication was completely out of proportion with what I was expecting. Here is the curious thing: the first night I saw the set, it was just wild. The second night, I became used to it. After a few nights, I became familiar with it. It was as if somehow I had seen it before. Of course I hadn’t. No one had seen it. No one had described it. The fact that a certain aspect of its mathematical nature remains mysterious, despite hundreds of brilliant people working on it, is the icing on the cake to me.
Benoit Mandelbrot [5]
Types Of Fractals In Nature
Even when doing an ordinary activity like strolling in a park or forest, fractal patterns are seen in many places in nature. The branching behavior that gives plants a self-similar shape also gives fractal repetition to trees, roots, leaves, ferns, and the fungal mycelium. If you are interested in all the details, check out my post about fractals in nature!
Geography also frequently displays fractal shapes. This was the key connection made by Carpenter in his landscape generation software. Fractals can also be found in the patterns of streams, rivers, coasts, mountains, waves, waterfalls, and water droplets in the natural world.
Here are some natural examples of types of fractal patterns in nature:
1. Fractals In Leaves And Plants
A lot of people never realize it, but since fractals are so common in nature it means they are common in food as well. The circulatory systems in the animal meat that we eat are fractal, and as we discussed since fractals are common in plants the patterns exist there too. Salads, broccoli, and pineapples are all great examples.
Just like the circulatory systems of animals, the self-similar patterns allow plants to distribute nutrients efficiently. The liquid water and electrolytes absorbed through the root structure flow through the plant and rehydrate the cytoplasm of each cell.
A form of broccoli known as Romanesco broccoli is one of the most notable examples. This form of broccoli has a fantastic structure of spires that radiate from a single point and branch out into their spires that extend to the plant’s tip.
2. Growth Spirals
Growth spirals, which follow the Fibonacci Sequence (also known as the Golden Spiral) and can be considered as a special case of self-similarity, also contain fractal patterns. The fractal pattern that is known as the Dragon Curve also relates to the Fibonacci Sequence since its Hausdorff dimension is the number φ (1.61803). You can learn to draw this fractal in my post about it.
3. Fractal Electricity and Lightning
If you’ve ever observed a lightning storm, you’ve seen one of nature’s most powerful displays of Fractals up close.
The fractal is the pattern generated when electricity passes through a medium that does not conduct electricity well (such as air).
Just like water in a river, the charge is trying to travel from the high point (in the cloud) to the low (the ground).
As the charge travels through the air, it is resisted. This resistance causes the current to fragment and split. The air becomes superheated when the current travels through it and the air glows brightly.
This process is repeated for each level of fragmentation until a fractal pattern emerges. When you reverse an image of a lightning strike or electrical discharge, you’ll find that it looks a lot like a tree. This is because they are both fractals.
Want to know more about an entire area of artwork that uses electrical fractal patterns for woodworking? Check out my post about the invention of Fractal wood burning!
4. Fractals in Human and Animal Bodies
Earlier we covered how biological systems like the circulatory systems and nervous systems follow fractal patterns.
Like how nutrients are efficiently distributed in plants, these patterns allow those systems to function rapidly. Another common location where fractal patterns exist is the human respiratory system.
The airway pattern begins with a single trunk (the throat, similar to a tree) that branches off in a self-similar pattern.
Each smaller network of cavities has its trunk which branches into a smaller and smaller network. This allows air to efficiently travel to where it is needed and swapped for carbon dioxide in the blood.
5. Fractals in Geography, Rivers, and Terrain
Rivers, like trees and plants, frequently fall into the Fractal category. When you consider how the terrain is produced and weathered, water erosion accounts for a significant portion of the landscape. Just like the lightning pattern, the water meets resistance and the river fractures into different similar parts.
Rivers and other bodies of water collect, transport, and distribute water throughout a landscape in the same way that fluids are distributed throughout a body. Water’s journey from a stream to a river, then to a lake or another huge body of water, is an excellent example. These also carry nutrients to the plants and farmland that depend on the river.
If you want to generate maps or digital landscapes of your own, check out my post about Wonderdraft! A computer generated map maker.
Fractals and Technology
Modern cell phones use a fractal antenna shape to work at multiple frequencies at the same time. Different forms correlate to the various radio bands that carry cell phone signals within the antenna.
Since these shapes are stacked within one another, multiple different frequencies can be used simultaneously in a cell phone.
According to research, fractal antennas outperform standard-shaped antennas, such as the old-fashioned whip antenna that used to be mounted on cars. If you want to learn more about this, check out my post on how fractals are used in technology.
Want Your Own Fancy Fractal Art? – I’ve Got You Covered!
Discover the most eye-popping artwork, clothing, and dog beds. Stop wasting time searching for less exciting alternatives! Impress your friends and loved ones while supporting the site in the process
Fractal image compression has been studied as a way to enhance the JPEG algorithm. The method used by JPEG is called a Discrete Cosine Transform which represents the image’s information in terms of frequency instead of pixel values. Since cosines are self-similar in shape, fractal image compression algorithms can then be used to recognize scaling patterns. These scaling patterns can then express the same frequency information as a smaller set of parameters for an iterated function system. [4]
Fractal image compression is also used in the compression of satellite data. If you can find repeated patterns in the data, you can use fractal equations for summarizing them, which are faster to communicate wirelessly than every pixel in the raw image.
To appreciate the nature of fractals, recall Galileo’s splendid manifesto that “Philosophy is written in the language of mathematics and its characters are triangles, circles and other geometric figures, without which one wanders about in a dark labyrinth.” Observe that circles, ellipses, and parabolas are very smooth shapes and that a triangle has a small number of points of irregularity. Galileo was absolutely right to assert that in science those shapes are necessary. But they have turned out not to be sufficient, “merely” because most of the world is of infinitely great roughness and complexity. However, the infinite sea of complexity includes two islands: one of Euclidean simplicity, and also a second of relative simplicity in which roughness is present, but is the same at all scales.
Benoit Mandelbrot [6]
Most Well-Known Fractals:
The two most famous fractals are The Mandelbrot Set and The Julia Sets.
The Mandelbrot Set
The Mandelbrot set, created by Benoit Mandelbrot, is the most well-known fractal in advanced mathematics, owing to its mesmerizing beauty. Since 1980, the set has served as a source of inspiration for artists, awe for kids, and a productive testing ground for the science of chaotic dynamics.
The set is a mathematical creation consisting of a seemingly oddly formed infinite collection of points concentrated on the complex number plane. In 1978, Robert W. Brooks and Peter Matelski defined and drew this set as part of a study of Kleinian groups. After that, in 1980, while working at IBM’s Thomas J. Watson Research Center in Yorktown Heights, New York, Benoit Mandelbrot created high-quality visualizations of the set.
Mandelbrot originally used his printer to render the images. As he investigated the relationship with Julia Sets, Mandelbrot first believed the printer to be rendering errors! We now know these sets as ‘Fatou Dust’.
The images of the Mandelbrot set have a complex and infinitely complicated boundary. Inside the boundary (the black points) correspond to the locations where the dynamics of the repeating function are stable and converge to a single shape. Outside the boundary (the multicolored regions) the dynamics are unstable and grow to infinity.
Since the points that can be chosen are real numbers that can be made arbitrarily small, the magnification can increase forever in finer detail. The boundary of the Mandelbrot set produces a fractal curve.
If you want to learn more about the Mandelbrot Set, check out my post about the most famous fractal!
Outside of the halls of academic departments, the Mandelbrot set is well known for its beautiful and unique visualizations. It is an example of taking a recursive function like the simple Mandelbrot equation and growing a complex structure by applying a few simple rules.
The Julia Sets
A Julia Set is another well-known fractal that is closely related to the Mandelbrot set. Julia Sets are substantially older than the Mandelbrot set because they were named after Gaston Julia. We covered his investigation of the iteration of polynomials earlier in the timeline, and his study of rational functions in the early twentieth century.
Julia Sets contain the points in which the iterations of the repeated function are stable. For linear discrete systems, this set is inside the unit circle on the complex plane. The shape of a Julia set depends on the initial condition parameter which is chosen for the nonlinear equation.
The Mandelbrot Set is a plot of these initial condition parameters and which values produce Julia Sets with stable (connected) shapes. If they are unstable, the shape is disconnected Fatou Dust.
Common Fractal Generation Techniques
The following are three basic methods for creating fractals:
1. Escape-Time Fractals
This type of fractal is produced by a recursively applied dynamic equation. Some examples of this type have been discussed already and are the Julia Sets and the Mandelbrot set.
Others included in this category include the Burning Ship fractal and Lyapunov fractal. These equations are often defined on an input space such as the complex plane.
2. Iterated Function Systems
Iterated function systems (IFS) have a geometric replacement rule that is fixed. IFS fractals include the Sierpinski carpet, Cantor set, Peano curve, Sierpinski gasket, Harter-Heighway dragon curve, T-Square, Koch snowflake, and Menger sponge. These fractals are also the type produced by visualization programs like Chaotica.
3. Random Fractals
Another class of fractal shapes originates from random (stochastic) processes. These processes were the type investigated by Mandelbrot’s advisor Paul Levy and cover Brownian motion, Lévy flight, and power laws.
The random movements appear to be the same and self-similar across magnitudes and time scales. The most commonly encountered examples of this type of fractal are stock and financial asset prices.
Fractal FAQs:
Fractal History Final Thoughts
Overall, researching fractals is a challenging yet fascinating topic of mathematics. Despite all of their complexities, they continue to be a helpful tool to model natural and chaotic systems. Hopefully, with the help of this article, you now have in-depth knowledge of the history of fractals.
Get Notified When We Publish Similar Articles
References
- Eglash, Ron. “Fractals in African settlement architecture.” Complexity 4.2 (1998): 21-29.
- Pickover, Clifford A. The math book: from Pythagoras to the 57th dimension, 250 milestones in the history of mathematics. Sterling Publishing Company, Inc., 2009.
- Mandelbrot, Benoit B., and Benoit B. Mandelbrot. The fractal geometry of nature. Vol. 1. New York: WH freeman, 1982.
- Gupta, R., D. Mehrotra, and R. K. Tyagi. “Adaptive searchless fractal image compression in DCT domain.” The Imaging Science Journal 64.7 (2016): 374-380.
- Mandelbrot, Benoit, and Valerie JAMIESON. “A fractal life.” New scientist 2473 (2004): 50-52.
- Obrist, Hans Ulrich. “The Father of Long Tails.” An interview with Benoît Mandelbrot (2008).