A fractal is a complicated geometric shape characterized by its roughness that displays properties of self-similarity at various scales. They are made by iterating on a simple rule in a continuous recursive loop. So you may come to wonder, what is the most famous fractal? This article will discuss everything you need to know about the most famous fractal in detail.
The Mandelbrot set’s boundary is the most famous fractal. The set is known for its stunning aesthetic beauty, as well as its deep significance for the study of dynamics and chaos theory. The set is generated from an incredibly simple rule and yet displays infinite depth and complexity.
Due to its captivating visual appearance, the Mandelbrot set has gained prominence with the general public outside of academic circles. Often, it is used as an example of something unique and interesting that can be created with math. The steps turn out to be pretty simple, and the computer does all of the work. Keep on reading to learn more about its history, usage, and importance.
History of Mandelbrot Set
Table of Contents
The theoretical background of the Mandelbrot set has its foundations in the field of dynamics. The goal is to define a point on the complex plane as a starting spot. Then, using that point as an input, repeatedly apply the same equation to generate new points at each time step.
The important question being solved is answering whether the points being generated ‘remain stable’ and stay within a certain area, or ‘blow up’ and go off to infinity. Spoiler: The black areas of the Mandelbrot set are starting points that remain stable, and the multicolored areas are starting points that blow up. Being able to answer this question is important for a ton of fields, including robotic automation and self-driving cars.
These dynamics were originally studied in 1918 by two mathematicians from France. These mathematicians were named Gaston Julia and Pierre Fatou. As a result, the sets are named Julia Sets, and the unstable and disconnected sets are called Fatou Dust. The Mandelbrot Set is named in honor of Mandelbrot and it was first printed in a paper in 1978 by Peter Matelski and Robert W. Brooks.
If you’re interested in the history of fractals like the Mandelbrot Set, check out my post on the history of fractals!
Benoit Mandelbrot’s Research
Benoit Mandelbrot initially saw a depiction of the set on March 1, 1980, at IBM’s Thomas J. Watson Research Center, New York.
In 1980, Mandelbrot investigated the parameter space of quadratic polynomials. In dynamic systems, the properties of quadratic polynomials can determine the stability properties of a system. Many of the Mandelbrot Set’s fundamental traits were developed by mathematicians John H. Hubbard and Adrien Douady, who named the set after Mandelbrot for his seminal work in fractal geometry.
You can check out the complete list of Mandelbrot’s books in my post covering the classics!
Spread of the Mandelbrot Set
Throughout the 1980s, the Mandelbrot Set rose in prominence from positive depictions in the press. This corresponded with an improvement in computer graphics and the ability to render the Mandelbrot Set in high resolution. It was often used as a demo of computer graphics ability at the time.
Two mathematicians created images and books about fractals and the Mandelbrot Set promoting it to the public. These mathematicians, Peter Richter and Heinz-Otto Peitgen compiled and presented an international touring exhibit for the Goethe-Institut in 1985.
The Mandelbrot Set got further coverage as the algorithm was first published on the cover of Scientific American in August 1985. Richter, Peitgen, and the Saupe University of Bremen all contributed to the design of the cover.
Contribution of Mathematicians
Douady and Hubbard’s findings caused a stir within the community, and the following period corresponded with a surge in mathematics abstracts related to complex dynamics.
A number of significant people have worked to contribute to understanding the Mandelbrot Set:
| Mathematician | Publication Year | Significant Mandelbrot Set Contribution | Link |
|---|---|---|---|
| Benoit Mandelbrot | 1982 | Developed and explored the theoretical framework | [1] |
| Adrien Douady and John Hubbard | 1984 | Proved the stable Julia Sets are fully connected among other advancements | [2] |
| Curt McMullen | 1984 | Studied rational maps and Kleinian groups and measured the Hausdorff dimension of some fractals | [3] |
| Adrien Douady | 1986 | Explored the relationship between Julia Sets and Mandelbrot Sets | [4] |
| Mitsuhiro Shishikura | 1994 | Studied the Hausdorff dimension of many fractals, including the Mandelbrot | [5] |
| Mikhail Lyubich | 1999 | Proved a conjecture about the Mandelbrot Set | [6] |
| John Milnor | 2000 | Examined the fixed points and orbits of the Mandelbrot Set | [7] |
| Jean-Christophe Yoccoz | 2003 | Continued the study of the dynamics of quadratic polynomials | [8] |
What is the Mandelbrot Set Used For?
As a general rule, the Mandelbrot Set marks all of the initial conditions for a given complex dynamic equation where the generated path has stable dynamics. For each dynamic equation, there is a corresponding Mandelbrot Set.
For each of these stable points, it means that the corresponding Julia Set which marks the stability boundary is fully connected (the set is not Fatou Dust).
When people refer to the Mandelbrot Set (the famous image), they are actually discussing the Mandelbrot Set for a specific simple dynamic equation. The equation which generates this set is:
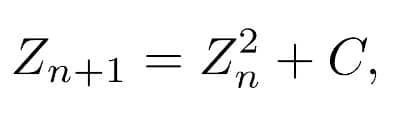
where C is the initial condition, and Z_n marks the location on the complex plane at time step n. Douady and Hubbard (in their work discussed earlier) were the first ones to prove that the stable Julia Sets were fully connected.
The boundary of the Mandelbrot Set is the famous fractal shape, and is not differentiable. Want to learn more about it? Check out my post on whether fractals are differentiable!
Why is the Mandelbrot Set Essential?
- It is possibly the most well-known and dramatic instance of how exceedingly simple rules can yield infinitely complicated effects. This was a huge surprise when it was discovered because it was previously assumed that you needed a complex system to produce complex behavior.
- The Mandelbrot set is generated using a very simple rule. It can be written in a few lines.
- The upshot of applying that rule is a shape of amazing intricacy that never ceases to amaze. It’s a fractal because you can uncover intricate patterns comparable to the whole thing no matter how far you zoom in.
- There is an infinite amount of diversity. It never repeats itself.
- The Mandelbrot set was discovered as computers became strong enough to allow us to see it clearly and appreciate its beauty. It would have been impossible to calculate it in inadequate detail in the past.
Want to know more about an entire area of artwork that uses fractal patterns for woodworking? Check out my post about the invention of Fractal wood burning!
The Haunting Beauty of the Mandelbrot Set
The set’s significance may stem from the fact that it’s become a strange attraction for scientists, artists, and the general public, all of whom may be drawn to it for quite different reasons. I certainly think it’s amazing for different reasons too!
The next thing which surprised us very much is that both for Julia sets and even more so for the Mandelbrot set, the complication was not, how to say, arbitrary, and almost everybody found the impression that these shapes were hauntingly beautiful.
Benoit Mandelbrot [9]
Scientists have been drawn to a new aesthetic that encompasses the artistic choices of color and detail they must make when examining the set, often with childlike enthusiasm.
The set’s haunting beauty drew artists and the general public in, and the idea of abstract mathematics was transformed into physical pleasures.
If you want to learn more about fractals and art, take a deep dive by reading this artistic article. If you want to make some fractal art of your own, learn how to draw fractals by hand.
Fibonacci Sequence in the Mandelbrot Set
There is a diagram called the Farey Diagram for understanding fractions and the Fibonacci sequence. Using this tool, you can see the Fibonacci sequence is contained in the Mandelbrot Set.
The relationship is reflected in the locations and number of the antennae which extend from the main bulb of the Mandelbrot set. These antennae follow the Fibonacci sequence of 1, 2, 3, 5, 8, 13, and 21. [10] I also discuss how this sequence appears in natural fractals. Check out my complete guide to fractals in nature!
Want to know how a fractal antenna is used in real life? Check out my article about fractals are used in technology and engineering.
Frequently Asked Questions
Famous Fractal Final Thoughts
The Mandelbrot Set has inspired its viewers for years as people appreciate both the visual and mathematical beauty of the fractal pattern. It has risen to become the most widely known and easily recognizable fractal picture. It has deep implications for complex dynamics and chaos theory. Hopefully, with the help of my article, you now have in-depth knowledge of the Mandelbrot set.
Get Notified When We Publish Similar Articles
References
- Mandelbrot, Benoit B., and Benoit B. Mandelbrot. The fractal geometry of nature. Vol. 1. New York: WH freeman, 1982.
- Douady, Adrien, and John H. Hubbard. “Exploring the mandelbrot set. the orsay notes.” Publ. Math. Orsay (1984).
- McMullen, Curt. “The Hausdorff dimension of general Sierpiński carpets.” Nagoya Mathematical Journal 96 (1984): 1-9.
- Douady, Adrien. “Julia sets and the Mandelbrot set.” The beauty of fractals. Springer, Berlin, Heidelberg, 1986. 161-174.
- Shishikura, Mitsuhiro. “The boundary of the Mandelbrot set has Hausdorff dimension two.” Astérisque 222 (1994): 389-405.
- Lyubich, Mikhail. “Feigenbaum-Coullet-Tresser universality and Milnor’s hairiness conjecture.” Annals of Mathematics (1999): 319-420.
- Milnor, John. “Periodic orbits, externals rays and the Mandelbrot set: an expository account.” Astérisque 261.xiii (2000): 277-333.
- Yoccoz, Jean-Christophe. “DYNAMICS OF QUADRATIC POLYNOMIALS.” Complex Dynamics and Geometry 10 (2003): 167.
- Benoit Mandelbrot, The haunting beauty in both the Julia set and Mandelbrot set. Retrieved April 15, 2022, from https://www.webofstories.com/play/benoit.mandelbrot/85
- Devaney, Robert L. “The Mandelbrot set, the Farey tree, and the Fibonacci sequence.” The American Mathematical Monthly 106.4 (1999): 289-302.